
PDF Publication Title:
Text from PDF Page: 004
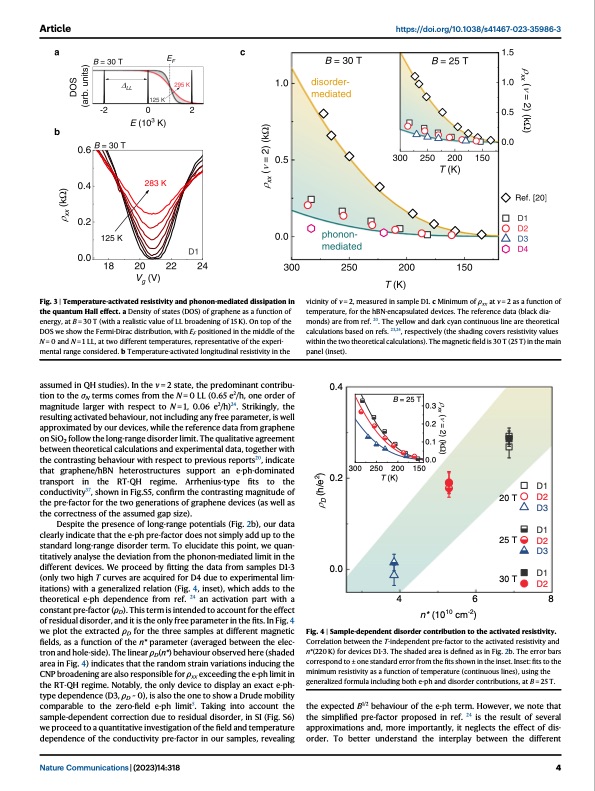
Article https://doi.org/10.1038/s41467-023-35986-3 Fig. 3 | Temperature-activated resistivity and phonon-mediated dissipation in the quantum Hall effect. a Density of states (DOS) of graphene as a function of energy, at B = 30 T (with a realistic value of LL broadening of 15 K). On top of the DOS we show the Fermi-Dirac distribution, with EF positioned in the middle of the N = 0 and N = 1 LL, at two different temperatures, representative of the experi- mental range considered. b Temperature-activated longitudinal resistivity in the assumed in QH studies). In the ν = 2 state, the predominant contribu- tion to the σN terms comes from the N = 0 LL (0.65 e2/h, one order of magnitude larger with respect to N = 1, 0.06 e2/h)24. Strikingly, the resulting activated behaviour, not including any free parameter, is well approximated by our devices, while the reference data from graphene on SiO2 follow the long-range disorder limit. The qualitative agreement between theoretical calculations and experimental data, together with the contrasting behaviour with respect to previous reports20, indicate that graphene/hBN heterostructures support an e-ph-dominated transport in the RT-QH regime. Arrhenius-type fits to the conductivity37, shown in Fig.S5, confirm the contrasting magnitude of the pre-factor for the two generations of graphene devices (as well as the correctness of the assumed gap size). Despite the presence of long-range potentials (Fig. 2b), our data clearly indicate that the e-ph pre-factor does not simply add up to the standard long-range disorder term. To elucidate this point, we quan- titatively analyse the deviation from the phonon-mediated limit in the different devices. We proceed by fitting the data from samples D1-3 (only two high T curves are acquired for D4 due to experimental lim- itations) with a generalized relation (Fig. 4, inset), which adds to the theoretical e-ph dependence from ref. 24 an activation part with a constant pre-factor (ρD). This term is intended to account for the effect of residual disorder, and it is the only free parameter in the fits. In Fig. 4 we plot the extracted ρD for the three samples at different magnetic fields, as a function of the n* parameter (averaged between the elec- tron and hole-side). The linear ρD(n*) behaviour observed here (shaded area in Fig. 4) indicates that the random strain variations inducing the CNP broadening are also responsible for ρxx exceeding the e-ph limit in the RT-QH regime. Notably, the only device to display an exact e-ph- type dependence (D3, ρD ~ 0), is also the one to show a Drude mobility comparable to the zero-field e-ph limit5. Taking into account the sample-dependent correction due to residual disorder, in SI (Fig. S6) we proceed to a quantitative investigation of the field and temperature dependence of the conductivity pre-factor in our samples, revealing vicinity of ν = 2, measured in sample D1. c Minimum of ρxx at ν = 2 as a function of temperature, for the hBN-encapsulated devices. The reference data (black dia- monds) are from ref. 20. The yellow and dark cyan continuous line are theoretical calculations based on refs. 23,24, respectively (the shading covers resistivity values within the two theoretical calculations). The magnetic field is 30 T (25 T) in the main panel (inset). Nature Communications | (2023)14:318 4 0.4 0.2 0.0 0.3 0.2 0.1 0.0 300 250 200 150 T (K) 468 n* (1010 cm-2) Fig. 4 | Sample-dependent disorder contribution to the activated resistivity. Correlation between the T-independent pre-factor to the activated resistivity and n*(220 K) for devices D1-3. The shaded area is defined as in Fig. 2b. The error bars correspond to ± one standard error from the fits shown in the inset. Inset: fits to the minimum resistivity as a function of temperature (continuous lines), using the generalized formula including both e-ph and disorder contributions, at B = 25 T. the expected B1/2 behaviour of the e-ph term. However, we note that the simplified pre-factor proposed in ref. 24 is the result of several approximations and, more importantly, it neglects the effect of dis- order. To better understand the interplay between the different D1 D2 D3 D1 25 T D2 D3 20 T 30 T D1 D2 B = 25 T xx( =2)(kΩ) D (h/e2)PDF Image | Phonon-mediated quantum Hall transport in graphene
PDF Search Title:
Phonon-mediated quantum Hall transport in grapheneOriginal File Name Searched:
s41467-023-35986-3.pdfDIY PDF Search: Google It | Yahoo | Bing
Salgenx Redox Flow Battery Technology: Power up your energy storage game with Salgenx Salt Water Battery. With its advanced technology, the flow battery provides reliable, scalable, and sustainable energy storage for utility-scale projects. Upgrade to a Salgenx flow battery today and take control of your energy future.
| CONTACT TEL: 608-238-6001 Email: greg@infinityturbine.com | RSS | AMP |